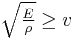Specific strength
The specific strength is a material's strength (force per unit area at failure) divided by its density. It is also known as the strength-to-weight ratio or strength/weight ratio. In fiber or textile applications, tenacity is the usual measure of specific strength. The SI unit for specific strength is (N/m2)/(kg/m3) or more commonly N·m/kg.
Another way to describe specific strength is breaking length, also known as self support length: the maximum length of a vertical column of the material (assuming a fixed cross-section) that could suspend its own weight when supported only at the top. For this measurement, the definition of weight is the force of gravity at the Earth's surface applying to the entire length of the material, not diminishing with height. This usage is more common with certain specialty fiber or textile applications.
The materials with the highest specific strengths are typically fibers such as carbon fiber, glass fiber and various polymers, and these are frequently used to make composite materials (e.g. carbon fiber-epoxy). These materials and others such as titanium, aluminium, magnesium and high strength steel alloys are widely used in aerospace and other applications where weight savings are worth the higher material cost.
Note that strength and stiffness are distinct. Both are important in design of efficient and safe structures.
Contents |
Examples
| Material | Strength (MPa) |
Density (g/cm³) |
Specific Strength (kN·m/kg) |
Breaking length (km) |
source |
|---|---|---|---|---|---|
| Scifer steel wire | 5,500 | 7.87 | 706 | 71.2 | [1] |
| Bainite | 2,500 | 7.87 | 321 | 32.4 | [1] |
| 1 μm iron whiskers | 14,000 | 7.87 | 1800 | 183 | [1] |
| Concrete | 10 | 2.30 | 4.35 | 0.44 | |
| Rubber | 15 | 0.92 | 16.3 | 1.66 | |
| Brass | 580 | 8.55 | 67.8 | 6.91 | [2] |
| Oak | 60 | 0.69 | 86.95 | 8.86 | [3] |
| Balsa (axial load) | 73 | 0.14 | 521 | 53.2 | [4] |
| Polypropylene | 80 | 0.90 | 88.88 | 9.06 | [5] |
| Nylon | 78 | 1.13 | 69.0 | 7.04 | [6] |
| Magnesium | 275 | 1.74 | 158 | 16.11 | [7] |
| Aluminium alloy (3003-H14) | 600 | 2.70 | 222 | 22.65 | [8] |
| Steel alloy | 2,000 | 7.86 | 254 | 25.93 | [8] |
| Titanium alloy | 1,300 | 4.51 | 288 | 29.38 | [8] |
| carbon-epoxy composite | 1240 | 1.58 | 785 | 80 | [9] |
| Silicon carbide | 3,440 | 3.16 | 1,088 | 110 | [10] |
| Glass fiber | 3,400 | 2.60 | 1,307 | 133 | [8] |
| Basalt fiber | 4,840 | 2.70 | 1,790 | 182.7 | [11] |
| Vectran | 2,900 | 1.40 | 2,071 | 211 | [8] |
| Carbon fiber (AS4) | 4,300 | 1.75 | 2,457 | 250 | [8] |
| Kevlar | 3,620 | 1.44 | 2,514 | 256 | [12] |
| Spectra fiber | 3,510 | 0.97 | 3,619 | 369 | [13] |
| Zylon | 5,800 | 1.54 | 3,766 | 384 | [14] |
| Colossal carbon tube | 6,900 | .116 | 59,483 | 6,066 | [15] |
| Carbon nanotube (see note below) | 62,000 | .037-1.34 | 46,268-N/A | 4,716-N/A | [16][17] |
| spider silk | 1,400 | 1.31 | 1,069 | 109 |
The data of this table is from best cases, and has been established for giving a rough figure.
- Note: Multiwalled carbon nanotubes have the highest tensile strength of any material yet measured, with labs producing them at a tensile strength of 63 GPa,[16] still well below their theoretical limit of 300 GPa. The first nanotube ropes (20 mm long) whose tensile strength was published (in 2000) had a strength of 3.6 GPa, still well below their theoretical limit.[18] The density is different depending on the manufacturing method, and the lowest value is 0.037 or 0.55(solid).[17]
Relation to velocity
Since N·m/kg (the unit of specific strength) expands to (kg·m/s2)·m/kg or (m/s)2, a specific strength can also be understood as the square of a speed, hence represented by it square root, a speed. Further, the structural analysis for whether a particular material is strong enough for some purpose can sometimes be expressed in terms of comparing this speed to the speed of a relevant part of the structure. For example, a spinning cylindrical shell (as in an idealized flywheel or an idealized cylinder space ship) is only feasible if built of a material whose square root of specific strength is at least the speed at which the spinning shell moves.
See also
References
- ^ a b c 52nd Hatfield Memorial Lecture: "Large Chunks of Very Strong Steel" by H. K. D. H. Bhadeshia 2005
- ^ RoyMech: Copper Alloys
- ^ Delft University of technology: Oak wood
- ^ [1]
- ^ Goodfellow: Polypropylene
- ^ Goodfellow: Polyamide - Nylon 6
- ^ eFunda: Magnesium Alloys
- ^ a b c d e f Vectran fiber: specific strength
- ^ McGRAW-HILL ENCYCLOPEDIA OF Science & Technology, 8th Edition, (c)1997, vol. 1 p 375
- ^ Specialty Materials, Inc SCS Silicon Carbide Fibers
- ^ http://www.albarrie.com/techfabrics/continuousfiber.aspx
- ^ Network Group for Composites in Construction: Introduction to Fibre Reinforced Polymer Composites
- ^ Spectra Fiber - Honeywell Advanced Fibers and Composites
- ^ Toyobo Co.,Ltd.. "ザイロン®(PBO 繊維)技術資料 (2005)" (free download PDF). http://www.toyobo.co.jp/seihin/kc/pbo/technical.pdf.
- ^ Peng, H.; Chen, D.; et al., Huang J.Y. et al. (2008). "Strong and Ductile Colossal Carbon Tubes with Walls of Rectangular Macropores". Phys. Rev. Lett. 101 (14): 145501. Bibcode 2008PhRvL.101n5501P. doi:10.1103/PhysRevLett.101.145501. PMID 18851539.
- ^ a b Yu, Min-Feng; Lourie, O; Dyer, MJ; Moloni, K; Kelly, TF; Ruoff, RS (2000). "Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load". Science 287 (5453): 637–640. Bibcode 2000Sci...287..637Y. doi:10.1126/science.287.5453.637. PMID 10649994.
- ^ a b K.Hata. "From Highly Efficient Impurity-Free CNT Synthesis to DWNT forests, CNTsolids and Super-Capacitors" (free download PDF). http://www.nanocarbon.jp/english/research/image/review.pdf.
- ^ "Tensile strength of single-walled carbon nanotubes directly measured from their macroscopic ropes" by F. Li, H. M. Cheng, S. Bai, G. Su, and M. S. Dresselhaus. DOI:10.1063/1.1324984
External links
- Specific stiffness - Specific strength chart, University of Cambridge, Department of Engineering